好书解读 | 《模拟计算指南》电子光谱：紫外-可见吸收光谱

《模拟计算指南》是唯理计算工程师团队沉淀7年实战经验、历时一年打造，是一本计算化学快速入门指南、材料模拟计算领域的实用宝典。

“书中详细介绍了从理论计算化学的基本原理到目前国际前沿应用体系的计算模拟思路和方法，有利于读者从多维度理解如何采用理论计算方法来解决复杂科学问题，并帮助初学者从中找到适合自己科研的理论支持和计算解决方案。”

——教育部长江学者、杰青、复旦大学教授

刘智攀

“本书以其实用性和易学性为特色，无论是计算物质科学的初学者还是资深研究者，都能从中获得独特的视角和丰富的知识资源，使其成为该领域内一本极具价值的入门及参考书籍。”

——教育部长江学者特聘教授、华南师范大学教授

赵纪军

↑扫码了解更多书籍及唯理计算信息

01文章介绍

今天我们介绍下《模拟计算指南》的5.2 电子光谱：紫外-可见吸收光谱。

光子的能量随频率遵循E=hv的关系。红外、拉曼等振动光谱的波数范围在几百到几千个cm⁻¹,通常不超过零点几个eV。 相比之下，紫外-可见吸收光谱中光子的能量高很多，其波长在几百个nm范围，光子能量达到了几个eV的量级，落在了电子激发态的能量区间。

理解电子激发态的电子结构的最浅显方式是在分子轨道的图像下将某些电子移动到高能轨道上(图5.6)。在基态下，所有电子填充在能量较低的轨道中；而将部分电子移动到未占据轨道后，将制造一系列能量较高的状态。视被激发的电子数量不同，可能有单电子激发、双电子激发等；激发后体系中存在多个成单电子，还可能有不同自旋多重度的激发态。

图5.6基于轨道占据而得到的激发态图像

这种对激发态电子结构的想当然描述虽然便于理解，但存在很大的缺陷：

(1)在这个过程中，假设基态和激发态的轨道不变，只是电子的排布发生了变化。然而电子排布变化势必导致电子间相互作用的改变，因此基态和激发态的“轨道”(如果轨道的概念仍然存在的话)应当是不同的。

(2)从第三章的介绍中我们已经知道，轨道本身就是单电子近似的产物，只有HF和DFT中存在轨道。真实分子的波函数也绝不是轨道函数的乘积。因此上述借助分子轨道理解激发态的方式完全依赖于单电子近似。与基态相比，激发态的电子结构更加复杂，单电子近似往往面临很大的挑战。事实上，各种主流激发态的计算方法都不再使用单电子近似来描述激发态，更不存在“轨道”的概念。某些文献中报道“激发态的轨道”,其实是激发态构型下的基态轨道。

此外，上述想当然的描述还容易给初学者带来一种错觉：如果基态和激发态的区别在于电子填充方式，那么两者的能量差是否等于电子填充情况发生改变的轨道之间的能量差?这个问题的答案明确是否定的。一方面轨道激发的图像并不正确，另一方面即使激发态完全是因为同一套轨道上电子在填充方式上的改变，但受电子间交换作用的影响，基态和激发态的能量差也不等于轨道的能量差。事实上，即使是在HF框架下，一个多电子体系的能量也不等于各占据轨道的能量之和。基态与激发态间的能量差与轨道能量差的差异被称为激子结合能(exciton binding energy)。一种常见的错误想法是，对于HOMO-LUMO激发，有人会试图通过HOMO-LUMO能级差推算激发能的数值甚至写出某些定量关系。由于激子结合能的存在，这些做法都是完全错误的。

综上所述，激发态的电子结构非常复杂。想要正确理解激发态的电子结构，并得到激发能及其他性质，必须针对激发态进行计算。对于绝大多数体系的尺度，TD-DFT(time-dependent DFT)是最主流的计算手段。

传统的DFT只能处理基态性质。TD-DFT在基态电子密度的基础上，可以得到激发态的能量和电子密度。Gaussian支持在TD-DFT水平下进行激发态的构型优化、频率和单点计算，对于给定结构，通过TD-DFT可以一次性求解任意个(只要计算资源足够)不同自旋多重度的激发态。显然，激发态计算比基态计算“昂贵”,通常其耗时比基态多一个数量级，并且考虑的激发态数量越多，消耗的计算资源就越多。接下来我们将分两节来介绍TD-DFT计算紫外-可见光谱的基本情况。在本节中，我们聚焦于吸收光谱。

吸收过程的时间尺度很短。根据不确定度关系，能量与时间的不确定度乘积与普朗克常数在同一数量级。将激发态能级的典型数值(几个eV)代入，可知吸收过程的时间尺度在阿秒(10^-18s)量级。如此短的时间内，分子的几何结构来不及改变，因此在绝大多数情况下认为吸收过程是在基态最优结构下发生的(垂直吸收)。因此，想要计算吸收光谱，只需在基态结构下进行TD-DFT单点计算即可。

吸收和发射过程均遵循自旋选律，只有自旋多重度不变的过程才是允许的。因此，对于单重态分子，想要考察吸收光谱，只需计算单重激发态。其他重态同理。吸收过程的强度使用振子强度(oscillator strength)描述，跃迁概率正比于振子强度的平方。在TD-DFT计算完成后，会输出指定数量的激发态的能级和振子强度。以所对应的光子波长为峰中心，通过振子强度得到峰高，进行展宽即可得到吸收光谱。

以4-二甲氨基苯基二氯三嗪为例，在TD-wB97xD/6-311G(d,p)水平下，对基态优化结构进行单点计算，将log文件用GaussView打开，右键Results→UV-Vis,可以得到吸收光谱(图5.7)。

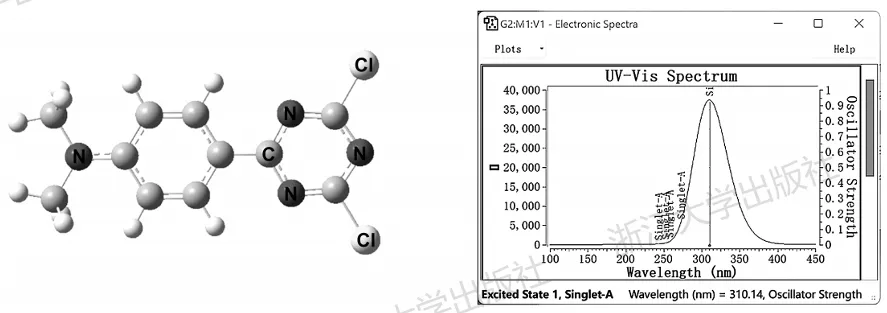
图5.7使用GaussView可视化得到的紫外-可见吸收光谱计算结果

输出文件中，关于激发态的信息如下所示：

图 4.7 NHC-Ag配合物的 ETS-NOCV 输出信息(部分)

其含义为，该分子的第一个单重激发态的激发能为3.9977eV,相当于310.14nm的光，振子强度为0.9225。随后的部分是轨道跃迁的组态系数，可以看到想要正确描述激发态，需要远远不止一对轨道激发。可以当作是大量不同的单电子近似框架下的单电子激发“成分”进行混合，才能正确描述一个激发态的性质。借助这些组态系数，可以近似得到某些轨道激发的成分占比，例如识别出“73->74”为HOMO/LUMO激发，其组态系数的平方除以全部电子激发组态系数的平方和，可以近似当作是HOMO/LUMO激发所占的比例。

在上述例子中，计算了5个单重激发态，其中S1有很高的振子强度，其余振子强度均为0,没有表现在吸收光谱中。S5态的波长大约为250nm,因此如果关心该分子在更短波长处的吸收行为，需要计算更多激发态，直到这些激发态囊括了感兴趣的波长。

在进行TD-DFT计算时，有如下几个问题是务必要注意的：

(1)务必关心分子结构是否正确。特别是某些分子在溶液中有多种存在形式，如不同的电离形态等，这些将显著影响分子的激发态性质，必须高度关注，绝不能想当然。如果这个分子在溶液中的主要存在形式是电离形态，而采用原始的未电离分子结构去计算，则结果势必南辕北辙。

(2)TD-DFT得到的激发态能级与泛函有关。总体上，泛函的HF成分越高，所得的波长越短。一些常用泛函的HF成分如表5.1所示。

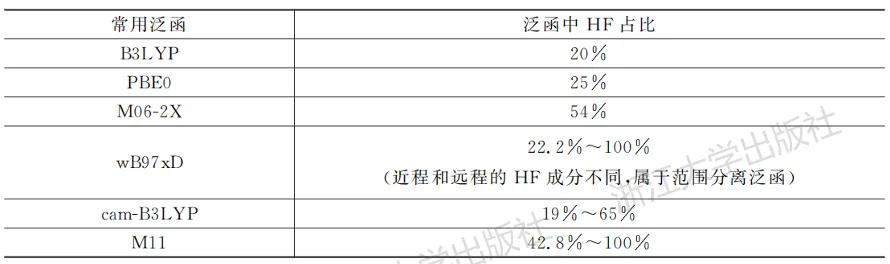
表5.1常用泛函中HF的占比情况

当一种泛函得到的结果与测定值偏差较大时，在确保结构正确的前提下，可以根据HF成分更换其他的泛函。需要注意的是，这种更换仍然要以泛函能够尽可能正确描述这类体系为准，不能为了凑一个接近测定值的波长数据而选择某些本身表现较差的泛函。通常也建议在上述主流的、普适性较强的泛函中进行选择。不含HF成分的纯泛函非常不适合用于TD-DFT计算。

(3)激发态的电子结构比基态更容易受到外界环境影响，因此对于溶液中的行为，应当尽可能考虑溶剂化。有的溶剂分子可以与待考察分子形成氢键等直接结合的，也应该在结构中予以适当的考虑。此时，可以对比原始结构以及与溶剂或体系中其他组分结合的结构，通过自由能计算得到相对含量，再对其光谱进行平均。

(4)HOMO-LUMO能级差与吸收波长无任何定量联系!这一点在之前已经介绍过了。除此之外，从普遍意义上来看，两者之间连定性关系也没有。只有当对比一些结构和激发态特征都比较相似的分子时，可以推断HOMO-LUMO能级差与激发态能级存在一定的联系，而如果实际结果表明两者不一致，也非常正常。只有直接进行激发态计算，才是判断激发态能量、结构、性质的可靠方法。

除了紫外-可见吸收光谱外，通过TD-DFT计算也可以得到电子圆二色谱(electronic circular dichroism，ECD)。电子圆二色谱是手性分子特有的性质，将圆二色谱的测定值与计算值进行对比，是确定手性分子绝对构型的重要方法。通过td=ecd关键字，可以让Gaussian输出给定结构的电子圆二色谱。圆二色谱呈现出上下波动的曲线状，对映体的圆二色谱严格呈现镜像，因此想要通过圆二色谱区分对映体时，主要关注曲线上下波动的趋势。与其他各种光谱相同，计算得到的圆二色谱同样是从峰中心位置人为任意展宽得到，因此可以调整展宽大小，以使得形状与测定值匹配。此外，也可以对谱图进行适当的平移和缩放，以便与测定结果对比。与吸收光谱相比，圆二色谱的一个重要特点是对构象非常敏感，因此大多数情况下需要计算多种构象，按照含量进行平均。这将在第7章进行介绍。

多位专家力荐  超全实战指南