好书解读 | 《模拟计算指南》核磁共振波谱

《模拟计算指南》是唯理计算工程师团队沉淀7年实战经验、历时一年打造，是一本计算化学快速入门指南、材料模拟计算领域的实用宝典。

“书中详细介绍了从理论计算化学的基本原理到目前国际前沿应用体系的计算模拟思路和方法，有利于读者从多维度理解如何采用理论计算方法来解决复杂科学问题，并帮助初学者从中找到适合自己科研的理论支持和计算解决方案。”

——教育部长江学者、杰青、复旦大学教授

刘智攀

“本书以其实用性和易学性为特色，无论是计算物质科学的初学者还是资深研究者，都能从中获得独特的视角和丰富的知识资源，使其成为该领域内一本极具价值的入门及参考书籍。”

——教育部长江学者特聘教授、华南师范大学教授

赵纪军

↑扫码了解更多书籍及唯理计算信息

01文章介绍

今天我们介绍下《模拟计算指南》的5.4核磁共振波谱。

核磁共振波谱是认识物质结构，特别是溶液中物质结构的最重要手段之一。通过对核磁的指认，可以鉴定化合物的几何结构；通过对化学位移的研究，可以加深对电子结构的认识。许多情况下，靠经验对核磁进行指认面临许多不确定性，人们会期望通过计算的手段协助对谱峰进行归属。

在Gaussian中，通过NMR关键字进行单点计算，可以得到给定结构中各原子核的磁屏蔽数值，与参比物质的磁屏蔽数值进行对照，即可得到化学位移。以氯仿为例，在M06-2X/def2-TZVP水平下进行构型优化，再在该水平下进行NMR单点计算，输出文件用Gauss-View打开，右键Results→NMR,即可查看“核磁谱图”,如图5.12所示。

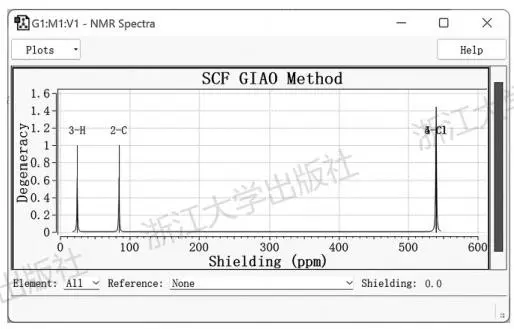
图5.12GaussView的氯仿的核磁共振计算结果可视化窗口

此处的横坐标是各向同性磁屏蔽数值，并未与参比物质对照，不是化学位移。想要快速得到化学位移，可以点击界面下方选择元素，GaussView内置了一些特定计算水平下的结果可以进行参比。如对于氢谱，选择以B3LYP/6-311+G(2d,p)水平下的四甲基硅烷(tetramethylsilane,TMS)为标准(GaussView还内置了HF水平下得到的磁屏蔽数值，这种数据质量太差，就不要选择了),立刻显示出了以化学位移为横坐标的谱图。此时得到氯仿中H的化学位移为7.45ppm(图5.13)。类似地，可以得到基于GaussView内置的参比数据，氯仿中碳原子的碳谱化学位移为97.8ppm。

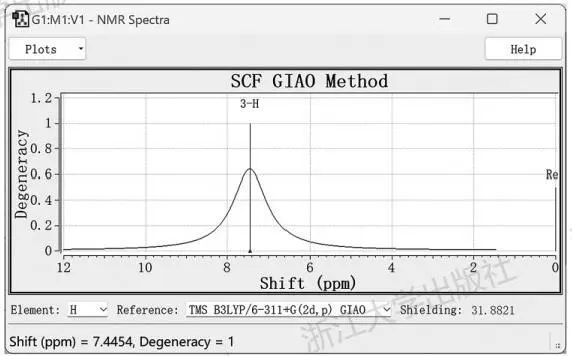
图5.13GaussView展示的氯仿的氢谱

众所周知，氯仿溶剂中残余氢的化学位移为7.26ppm。自然而然地，我们会想，如果在相同计算水平下去算一遍TMS的磁屏蔽数值来作为参比，是否会有更好的结果?遗憾的是，事实上并没有更好，以M06-2X/def2-TZVP水平下的TMS的磁屏蔽数值作为参比，氯仿中H的化学位移变成了7.54ppm。因此，通过一般的DFT计算想要将核磁化学位移算准并不容易，一般用于比较不同化合物之间或同一化合物不同磁性核之间化学位移的变化情况较为合适；同时，当一张核磁谱图可能与多种结构对应时，也可以通过计算比较哪个结构的计算结果与测定结果最为接近。如在一项近期的全合成工作中[33],Suenaga等人即采取了这种做法，通过对多种可能结构的计算核磁谱图与测定结果的平均偏差进行对比，再结合ECD等其他光谱的计算，最终从多个可疑结构中得到了比较确定的答案。

除了上述直接计算的方法外，对于氢谱和碳谱，还有一种方便而准确的方法可用于得到化学位移：标度法。标度法的基础在于经过大量实践发现，虽然用DFT直接得到准确的核磁化学位移有难度，但计算值与测定值往往存在不错的线性关系，因此只要对于固定的计算水平拟定好一套回归系数，就可以很好地再现测定值。此外，revTPSS/pcSeg-1水平对于常见化合物的核磁化学位移计算也有较好的精度。在http://cheshirenmr.info/ScalingFac-tors.htm上，汇总了一系列前人拟合的标度法回归系数，如图5.14所示。

图5.14标度法回归系数(部分)

如果要使用标度法，则需要在其中注明的计算水平下进行构型优化和NMR单点计算，再将得到的磁屏蔽数值代入线性回归公式。对于常见化合物，此法的准确度往往高于直接计算。

多位专家力荐  超全实战指南

↑扫码了解更多书籍及唯理计算信息