【摘要】 核磁共振成像系统的构成介绍

本期我们对核磁共振成像系统的构成的进行介绍。

1 I如果获取了二维傅立叶变换的所有值F(kx， ky,),就可以用计算机运用公式对F(kx,ky,)作反傅立叶变换获取f(kx,ky)所描述的空间称为K空间。在K空间某个点f(xn,xm)的值的含义是图像中f(xn,xm)沿着x方向以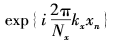形式变化，且沿y方向以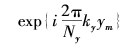形式变化的成分。

一、核磁共振二维傅立叶成像

在核磁共振成像中，要进行二维成像，先要用射频电场和梯度磁场选择一个成像层面(前面已经讲过)。选择了成像层面后，此时层面内的自旋合成总磁矩在平面内有不为零的分量即横向磁化矢量,标为Mxy。在磁场均匀且无附加磁场的情况下，Mxy,会以拉莫尔进动频率0o绕z轴进动，即在xoy平面内绕z轴旋转。如果选择一个以同样频率w0旋转的坐标系(x轴、y轴绕z轴旋转)，则在新的坐标系下，Mxy,就固定不动(磁场均匀且无附加磁场时)，这样可以使分析比较简

1.二维傅立叶成像的原理

前面提到，通过射频电磁场及垂直于成像层面的梯度磁场，可以选择成像层面。选择完成像层面后，此时检测到的信号是成像层面内总的Mxy，还无法获取各个位置(x，y)处的M,(x，y)值。此时需要加载如图1所示的梯度磁场区分不同的像素子区。假设我们要成像的区域沿x轴、y轴方向为FOVx.及FOVy,，分辨率为Nx,

则像素大小△x，△y为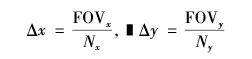

 

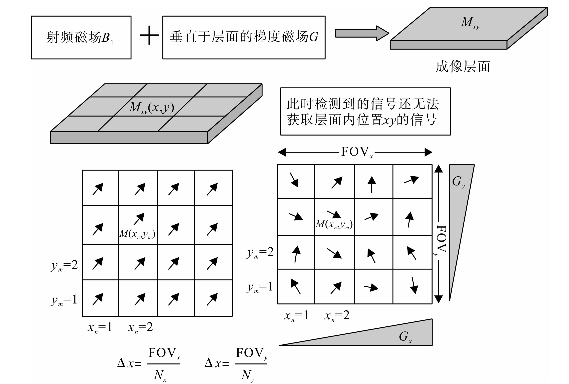
图1利用梯度磁场可以区分出不同位置的合成自旋磁矩即Mx,y,(x, y)

 

假设每单个像素中的微观磁矩合成的局部宏观磁矩即磁化矢量为Mxy(xn,ym)。

 

本期由于版面有限，我们将在下一期继续进行向大家进行介绍。

 

参考文献

[1]赵喜平. 磁共振成像系统的原理及其应用. 科学出版社, 2000.