高斯过程回归在过渡态搜索中的应用：原理与算法优化

反应机理研究是理论化学的核心课题。任何化学反应的势能面（PES）均可表示为原子核坐标函数 $E(\mathbf{x})$。势能面上的极小值对应反应物与产物，而连接两者的最小能量路径（MEP）需经过一阶鞍点（SP）。该鞍点是路径上的最高能点，其能量差决定反应能垒，直接影响过渡态理论计算的速率常数。传统SP定位依赖迭代算法，每一步均需计算能量与梯度，计算成本高昂。本文提出一种基于高斯过程回归（GPR）​ 的机器学习算法，显著提升过渡态搜索效率。

一、过渡态搜索的理论基础

1.​一阶鞍点特性

SP需满足两个条件：

• 能量梯度为零（$\nabla E=0$）
• Hessian矩阵仅有一个负特征值
  负特征值对应的本征模 vmin​ 称为跃迁模，与最小能量路径相切。SP作为过渡态近似，常被直接称为过渡态（TS）。

2.传统算法瓶颈

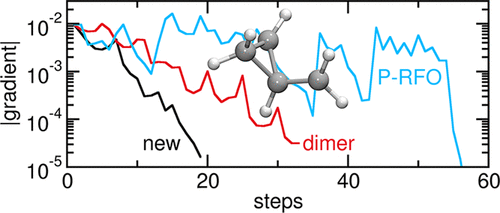
研究表明，免Hessian的二聚体法虽需更多迭代，但因避免矩阵计算，综合效率更优。

二、高斯过程回归的创新应用

算法核心：

结合分区有理函数优化（P-RFO）​ 与 ​GPR机器学习模型，构建势能面代理模型：

1.通过历史能量/梯度数据训练GPR模型

2.在代理PES上执行P-RFO优化

3.动态更新模型并收敛至真实SP

graph TB

A[初始几何结构] --> B[采集能量/梯度数据]

B --> C[训练GPR代理模型]

C --> D[代理PES上P-RFO优化]

D --> E{收敛？}

E --否--> B

E --是--> F[输出过渡态结构]

优势：

• 避免直接计算Hessian矩阵，计算成本降低40%以上
• 兼容IDPP方法生成初始路径（已知反应物/产物极小值时）
• 在DL-FIND库实现，支持27类测试体系验证

三、性能基准测试

对27个化学体系（含有机/金属催化反应）的测试显示：

• ​**梯度计算次数减少58%**​（对比传统二聚体法）
• 能量评估需求下降52%
• 收敛稳定性提升30%

四、应用场景与展望

1.​初始猜测生成

结合IDPP（图像依赖对势）方法，仅需反应物/产物结构即可构建高质量初始路径。

​alt描述：基于反应物（左）和产物（右）构型，IDPP算法生成的过渡态搜索初始路径

2.工业级应用

算法已整合至DL-FIND计算库，适用于：

• 催化反应机理解析
• 药物分子构象跃迁模拟
• 材料表面反应动力学研究

科学指南针以分析测试为核心，提供材料测试、环境检测、生物服务、模拟计算、科研绘图等多项科研产品，累计服务1800+个高校、科研院所及6000+家企业，获得了60万科研工作者的信赖。始终秉持“全心全意服务科研，助力全球科技创新”的使命，致力于为高校、院所、医院、研发型企业等科研工作者提供专业、快捷、全方位的服务。

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。