霍尔效应-相关效应

1.整数量子霍尔效应

德国科学家冯·克利青发现，在极低温度1.5K和强磁场18.9T条件下，测量金属—氧化物—半导体场效应晶体管时，发现随磁场的变化，霍尔电阻R _H 出现了一系列量子化数值，即：

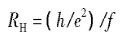
式1

式中， h为普朗克常数，f为正整数，e为电子电量。这种现象被称为整数量子霍尔效应，这与经典霍尔效应理论中的霍尔电阻随磁场连续变化并随着载流子浓度的增大而减小相矛盾。

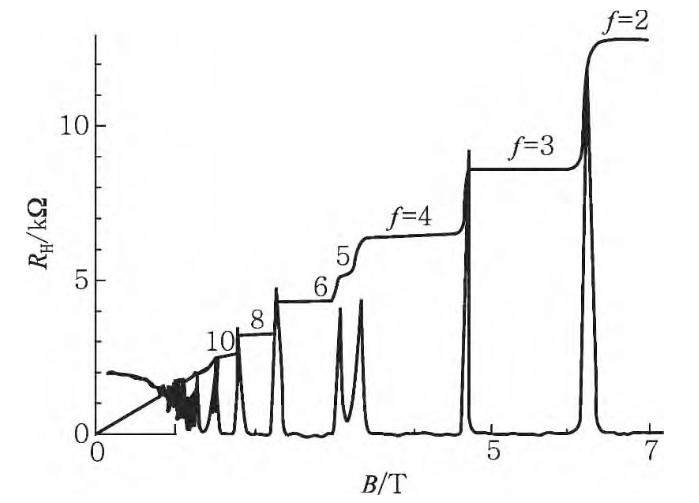
图1 整数量子霍尔效应的RH-B图

如图1所示，下边带峰的曲线表示纵向欧姆电阻，当霍尔电阻处于某一平台值时，所对应的纵向电阻等于零，由于填充因子f是量子化的，所以该效应称为量子霍尔效应，又因f取整数，故又称之为整数量子霍尔效应。

整数量子霍尔效应的机理可用“朗道能级”及“边缘态”进行解释：（1）按经典电磁理论，处于强磁场中的电子在洛伦兹力作用下作圆周运动形成回旋轨道，使样品中间成为绝缘体。这些电子圆轨道是量子化的，且具有分立的能级。某一时刻，电子按泡利不相容原理共填充了f (为正整数) 个朗道能级，此时得到的霍尔电阻平台, 正好对应 (h/e²) /f。（2）霍尔电阻处于某一平台值时，电流流过样品而无纵向电阻。其原因是在样品边缘的电子虽然也受洛伦兹力而作圆周运动，但还未完成一个圆周运动就被边缘反弹回来，然后继续圆周运动，继续反弹，这个过程反复进行，电子就可沿样品的边缘从一端运动到另一端，形成“边缘态”。由于外加磁场的作用，电子只能沿着一个方向运动，边缘的电子当碰到杂质时，会绕一个弯继续向前，不会发生散射，由于散射是电子能量耗散形成电阻的主要原因，所以在量子霍尔态电子的运动是无能量损耗的，即电流流过样品而无纵向电阻。

[1] 王东,浅谈从霍尔效应到量子反常霍尔效应[J]. 电子世界. 2016,(23)

[2] 李海, 量子霍尔效应及量子反常霍尔效应的探索历程[J]. 大学物理. 2014,33(12)

[3]乔振华. 三维量子霍尔效应验证探索[J]. 科技成果管理与研究, 2020(7):3.

[4]阳新蕃. 克劳斯·冯·克利青和量子化霍尔效应—1985年诺贝尔物理学奖简介[J]. 武汉大学学报(自然科学版), 1986(01):129-130.