【摘要】 采用梯度校正的非定域或广义梯度近似泛函与电子密度梯度 dρ/dr 和电子密度 ρ 都有关，这样可以同时提高能量和结构预测的准确性，但计算耗时。

 

采用梯度校正的非定域或广义梯度近似泛函与电子密度梯度 dρ/dr 和电子密度 ρ 都有关，这样可以同时提高能量和结构预测的准确性，但计算耗时。CASTEP 中提供的非定域泛函有三种：PBE 泛函与 PW91泛函计算在本质上实际是相同的，但在电子密度变化迅速体系中 PBE 泛函实用性更好；RPBE 是特别用来提高 DFT 描述金属表面吸附分子能量的泛函，White and Bird 描述了各种梯度校正泛函计算方法，利用广义梯度近似计算总能量使用平面波基组与定域泛函相比并不直接。包含梯度近似的交换-相关泛函计算时对电子密度数据的精度要求较高，对计算机内存占用会增大。通过采用与平面波基组总能量计算中分裂交换-相关能量采用一系列空间网格相一致的方法来定义交换-相关势。

 

平面波基组（Plane wave basis set）

 

Bloch 理论表明每个 k 点处电子波函数都可以展开成离散的平面波基组形式，理论上讲这种展开形式包含的平面波数量是无限多的。然而相对于动能较大的情况，动能|k+G|2很小时平面波系数 Ck+G更重要。调节平面波基组，其中包含的平面波动能小于某个设定的截止能量，如下图所示（球体半径与截止能量平方根成比例）：

 

 

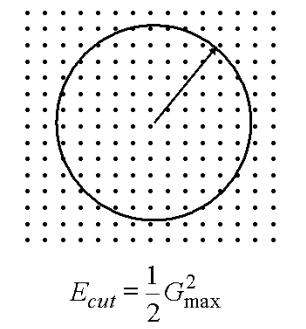
总能量计算会因为平面波特定能量截止而产生误差，通过增加体系能量截止数值就可以减小误差幅度。理论上截止能量必须提高到总能量计算结果达到设定的精确度为止，如果你在进行关于相稳定性的研究，而需要对比每个相能量的绝对值时，这是一种推荐计算方法。不过，同一个结构在低的截止能量下收敛引起的差别要小于总体能量本身。因此可以选用合适的平面波基组对几何结构进行优化或进行分子动力学研究。以上的方法对 Brillouin区取样收敛测试同样成立。

 

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。