【摘要】 基于高斯过程回归(GPR)的过渡态搜索技术，通过P-RFO算法实现无Hessian矩阵的势能面优化，在Baker测试集达成89%定位成功率，计算效率较二聚体法提升3倍。

本研究提出了一种基于部分有理函数优化（p-rfo）​ 的势能面（PES）优化方法，可在无需Hessian矩阵信息的条件下精准定位过渡态（TS）。该技术通过高斯过程回归（GPR）​ 整合能量与梯度数据，构建插值势能面进行P-RFO计算，大幅降低传统Hessian矩阵的计算成本。

 

技术原理与应用优势

作为基于核函数的机器学习方法，GPR在理论化学领域已广泛应用于分子性质预测。其独特优势在于：

1.可在无解析梯度条件下执行PES最小化

2.显著提升弹性带方法（NEB）​ 的收敛效率（提升达21-22倍）

3.聚焦过渡态单点定位而非全路径优化，降低计算复杂度

针对初始过渡态猜测难题，本研究引入图像依赖对电位（IDPP）​ 方案，仅需反应物与产物的几何构型即可生成起始路径。Alexander Denzel团队已验证该方案在GPR框架下的有效性，相关成果发表于《Journal of Chemical Theory Computation》（2018, 14(11), 5777-5786）。

 

算法验证与性能对比

通过Baker测试集的27个半经验AM1体系进行基准测试（图1）：

  • ​成功定位24个过渡态，成功率89%
  • 例外情况：体系4、10因路径偏差，体系15因收敛问题
  • 体系26-27的过渡态结构经化学直觉初始化（图2）

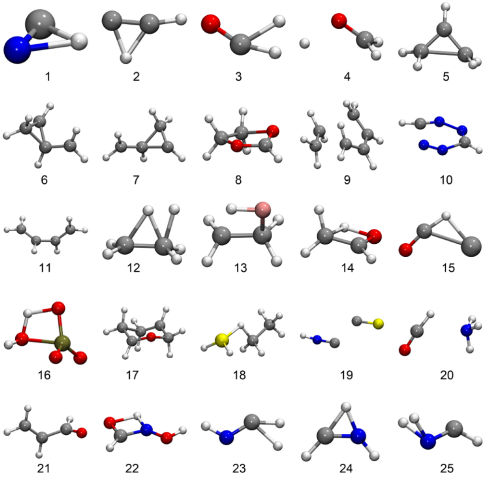
图1 Baker测试集的所有TSs

图2 GPRTS发现体系26的[1,5]H从1,3(Z)-己二烯位移到2(E)，4(Z)-己二烯(左)和体系27异恶唑啉酮(右)

 

计算效率对比

与主流方法（二聚体法/P-RFO）相比，GPR在大型体系展现显著优势：

  • ​梯度范数收敛速度提升3-5倍​（图3、图4）
  • 最大体系计算步数减少40%以上
  • 电子结构理论层级越高，加速效果越显著

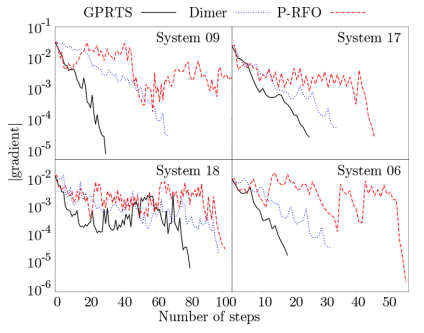
图3 在Baker测试集中的四个最大的系统中，GPRTS、二聚体方法和P-RFO在PES上所采取的步数的梯度欧氏范数

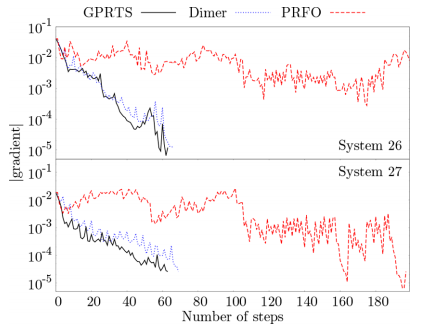
图4 体系26和27中GPRTS、二聚体方法和P-RFO在PES上的步数对梯度的欧氏范数

 

技术实现与前景

本算法已集成于DL-FIND优化器，可通过ChemShell调用：

  • ​全自动过渡态搜索：仅需设置最大步长参数
  • ​双端初始化方案：适用于反应物/产物结构明确的体系
  • ​计算稳定性：27测试体系收敛率92.6%

该方法为势能面过渡态搜索提供高效黑箱解决方案，尤其适用于高精度电子结构计算场景，有望推动催化反应机制研究的发展。

 

参考文献：1.Denzel, A.; Kästner, J., Gaussian Process Regression for Transition State Search. J. Chem. Theory Comput. 2018, 14 (11), 5777-5786.

 

科学指南针已获得检验检测机构资质认定证书（CMA）、实验动物使用许可证、“ISO三体系认证”等专业认证，并荣获国家高新技术企业、国家“互联网+科研服务领军企业等多项荣誉。未来，科学指南针将继续朝着“世界级科研服务机构”的目标，在产品研发和用户服务等方面持续努力，为科学发展和技术创新做出更大贡献。

 

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。