【摘要】 对于DFT计算，采用RSPACE代码，该代码在DFT框架内使用实空间有限差分方法，使我们能够研究由于边界条件的高度自由度而导致的输运性质。

石墨烯是一种具有双部蜂窝细胞（BHC）的二维材料，作为下一代电子材料一直是广泛研究的主题。石墨烯的价带和导带表现出一种称为狄拉克锥的特征带结构。

 

Mitsuharu Uemoto等人[1]利用石墨烯中的两个谷的Valleytronics吸引了相当多的关注，谷滤波器有望成为Valleytronics的核心组件。从而该研究提出利用气泡缺陷的石墨烯谷过滤器，通过密度泛函理论计算来研究石墨烯的Stone - Wales和气泡缺陷的谷相关输运性质。发现在某些缺陷中，从K谷到K谷的谷间跃迁完全被抑制。

 

其利用一个包含多个碳原子的大双部蜂窝细胞，用分子轨道代替原子轨道，在紧密结合模型中证明了双部蜂窝细胞a和B位点之间的对称性有助于抑制谷间跃迁。使用密度泛函理论（DFT）计算方法，研究了石墨烯中具有SW和水泡缺陷的谷相关输运特性，如图1和图2在SW缺陷结构(S1和S2)中，提出了适用于谷滤波器的水泡缺陷。

 

 

图1 (a) S1和(b) S2结构散射区的原子结构。

 

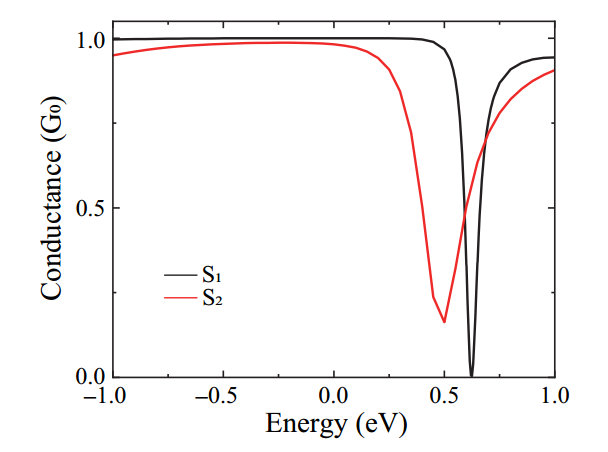
图2 SW缺陷的电导谱

 

对于DFT计算，采用RSPACE代码，该代码在DFT框架内使用实空间有限差分方法，使我们能够研究由于边界条件的高度自由度而导致的输运性质。给出了嵌入SW缺陷并沿x轴正方向注入电子的散射区域的计算模型。

 

首先，在常规的周期边界条件下，使用超级电池研究了无缺陷石墨烯和有缺陷石墨烯的优化原子结构。计算区域设为19.68 × 17.04 × 10.58˚A3, 128 × 80 × 50个网格点，在布里因区域取一个6 × 6的Monkhorst-Pack网格，包含Γ-point。交换相关效应由DFT的局部密度近似处理，并使用投影增广波方法来描述电子-离子相互作用。

 

然后，我们通过将石墨烯电极连接到散射区域的左右两侧来检查缺陷结构的谷依赖输运性质。在为获得散射波函数而进行的输运性质计算中，采用了Troullier和Martins的保范赝势。为了确定Kohn-Sham有效势，在周期边界条件下使用超级单体，然后在非自一致的半无限边界条件下计算散射波函数。据报道，该过程在线性响应状态下同样准确，但比在散射波基础上进行自一致计算要有效得多。

 

对布里渊区积分采用Γ点作为散射区域，电极区域的k点网格与散射区域的k点网格相对应。研究了缺陷的输运特性与缺陷局部原子结构之间的关系。

 

结果发现，虽然BHCs在某些缺陷中存在畸变，但其谷间转变被完全抑制。利用含有多个碳原子的LBHC，用分子轨道代替原子轨道，在紧密结合模型中证明了结构缺陷的对称性破缺导致了谷间跃迁。此外，还推导出了抑制谷间跃迁的泡泡原子结构的普遍规律。

 

此外，通过向石墨烯中引入额外的碳原子来形成泡状缺陷。研究发现，由于碳原子的加入，K和K′通道电子共振散射态的能量在泡状缺陷（C2、C4和C6）中发生分裂。谐振状态的分裂将使其能够通过在泡泡区域局部施加栅极电压来实现全谷极化电流。

 

[1]. Uemoto, M.;  Nishiura, M.; Ono, T., Valley filters using graphene blister defects from first principles. JOURNAL OF PHYSICS-CONDENSED MATTER 2024, 36 （9）.

 

科学指南针以分析测试为核心，提供材料测试、环境检测、生物服务、模拟计算、科研绘图等多项科研产品，累计服务1800+个高校、科研院所及6000+家企业，获得了60万科研工作者的信赖。始终秉持“全心全意服务科研，助力全球科技创新”的使命，致力于为高校、院所、医院、研发型企业等科研工作者提供专业、快捷、全方位的服务。

 

免责声明：部分文章整合自网络，因内容庞杂无法联系到全部作者，如有侵权，请联系删除，我们会在第一时间予以答复，万分感谢。